一文读懂：霍夫曼编码

摘要

1951年，David A. Huffman还在麻省理工学院攻读博士学位，在信息论课程的学期报告中，他创新性地发明了一种二进制编码方法，并于次年发表在他的论文《一种构建极小多余编码的方法》中。而这种特殊的二进制编码方法，正是霍夫曼编码。

霍夫曼编码是一种无损数据压缩技术。如今，在图像、视频、文件、互联网数据等对象的压缩中，都有它的身影。在这篇博客中，我们将深入探究霍夫曼编码的原理，并严格证明该编码的最优性。

基本原理

霍夫曼编码的基本原理并不复杂：对于一段文本来说，它先通过概率统计的方法计算出每个字母出现的概率，对于出现概率较高的字母，则使用较短的编码，反之，对于出现概率较低的字母，则使用较长的编码。如是，这段文本在计算机中编码长度的期望值便大大降低，从而起到无损压缩数据、节省存储空间的作用。

在我们先前的文章了解字符编码：ASCII、UTF-8中，我们提到了字符编码可容纳的信息与其所占用空间之间的矛盾，也介绍了Unicode是如何通过可变长度编码(VLE)来化解这一矛盾的。而本文的主角：霍夫曼编码，并不依赖于固定的编码长度，也不依赖于特殊前缀而界定截断位置，更巧妙地，它使用一棵满二叉树实时生成文本对应的编码，并且可以保证任何一个字符的编码不会成为其他字符编码的前缀（这样的编码我们称为前缀编码，也有的人凭直觉称之为无前缀编码，本文中我们采用前者），从而规避了读取二进制位时的截断问题。

接下来，我们将详细介绍并证明霍夫曼编码是如何达到这样的效果的。

编码流程

1. 计算字符频次

对于一段数据，例如下方样例中的字符串，我们先对其进行遍历，统计出每个字符的出现频率。

let str = "aaabbc";
let freq = {};

for (let i = 0; i < str.length; i++) {
  let char = str.charAt(i);
  if (freq[char]) {
    freq[char]++;
  } else {
    freq[char] = 1;
  }
}

2. 构建优先队列，存放节点

在该步骤中，我们将创建一个优先队列，并存放每个字符对应的节点。每个字符节点由字符与该字符对应的频率组成。

let nodes = [];

for (let char in freq) {
  nodes.push({ char, freq: freq[char], left: null, right: null });
}

3. 构建霍夫曼树

该步骤涉及的原理较为复杂，简而言之，我们在步骤2中优先队列的基础上，重复选择队列中频率最低两个节点，将其组合，并将这两个节点的频率值进行求和，作为新节点的频率值，紧接着，这个新节点将连接着两个子节点，被放入优先队列中。最后，当队列中只存在一个根节点时，我们便得到了一棵满二叉树，在这里，我们称其为霍夫曼树：文本中出现的每个字符都可以在霍夫曼树的叶子上找到，并且在遍历霍夫曼树的过程中，我们可以得到对应字符的霍夫曼编码（亦即步骤4）。

例如，对于我们样例中的字符串:

aaabbc

即以下三个节点:

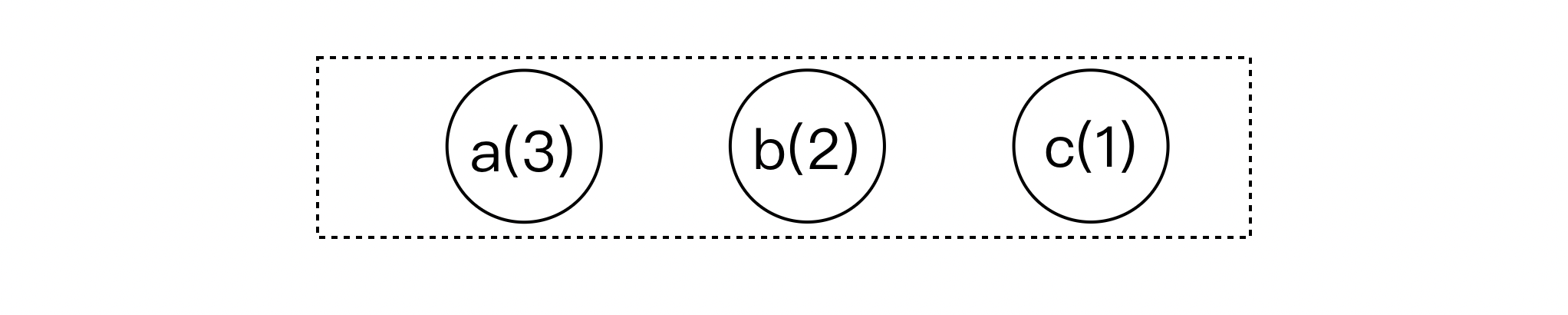
其对应的霍夫曼树生成步骤为：

1. 选中队列中频率最低的两个节点

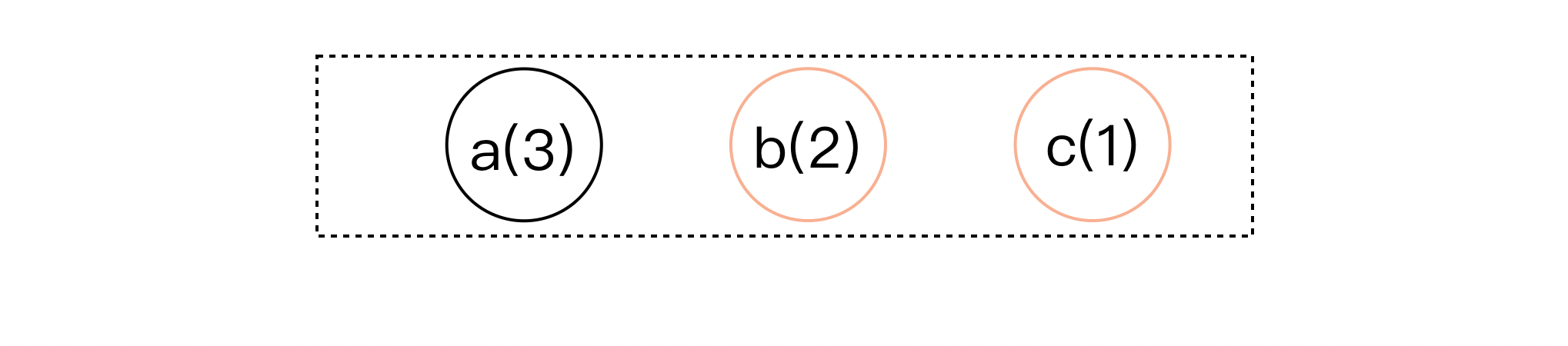
2. 将其合并为一个节点，这两个节点的父节点对应的频率值为二者求和

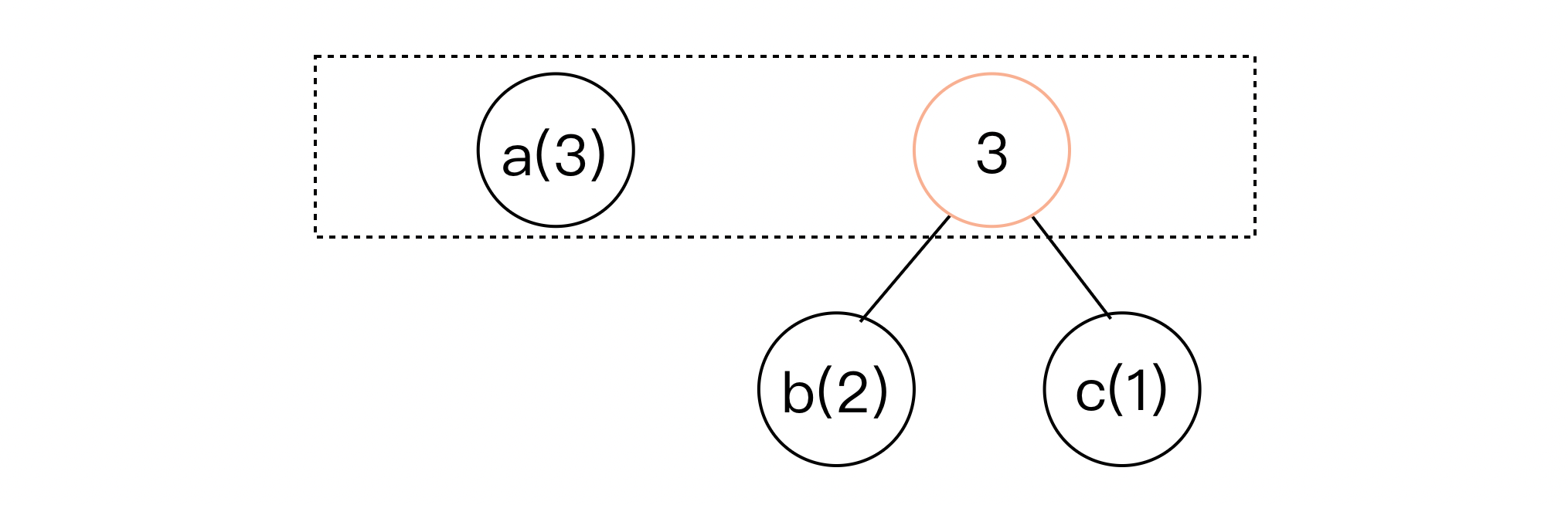
3. 再次选中队列中频率最低的两个节点

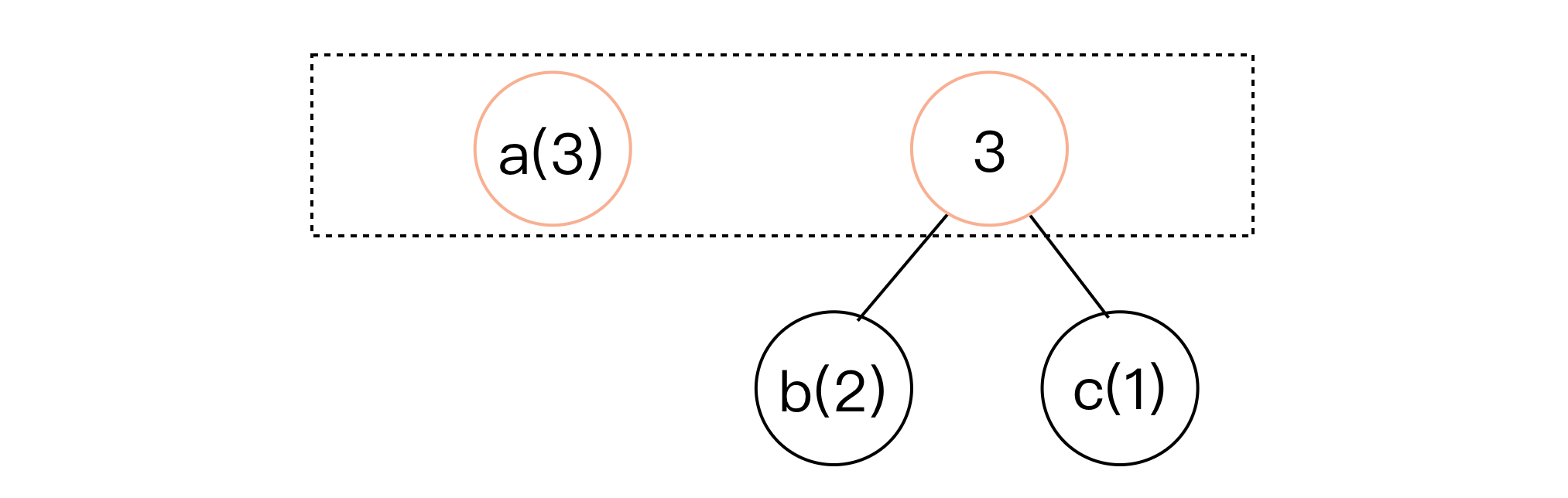
4. 将其合并为一个节点，这两个节点的父节点对应的频率值为二者求和

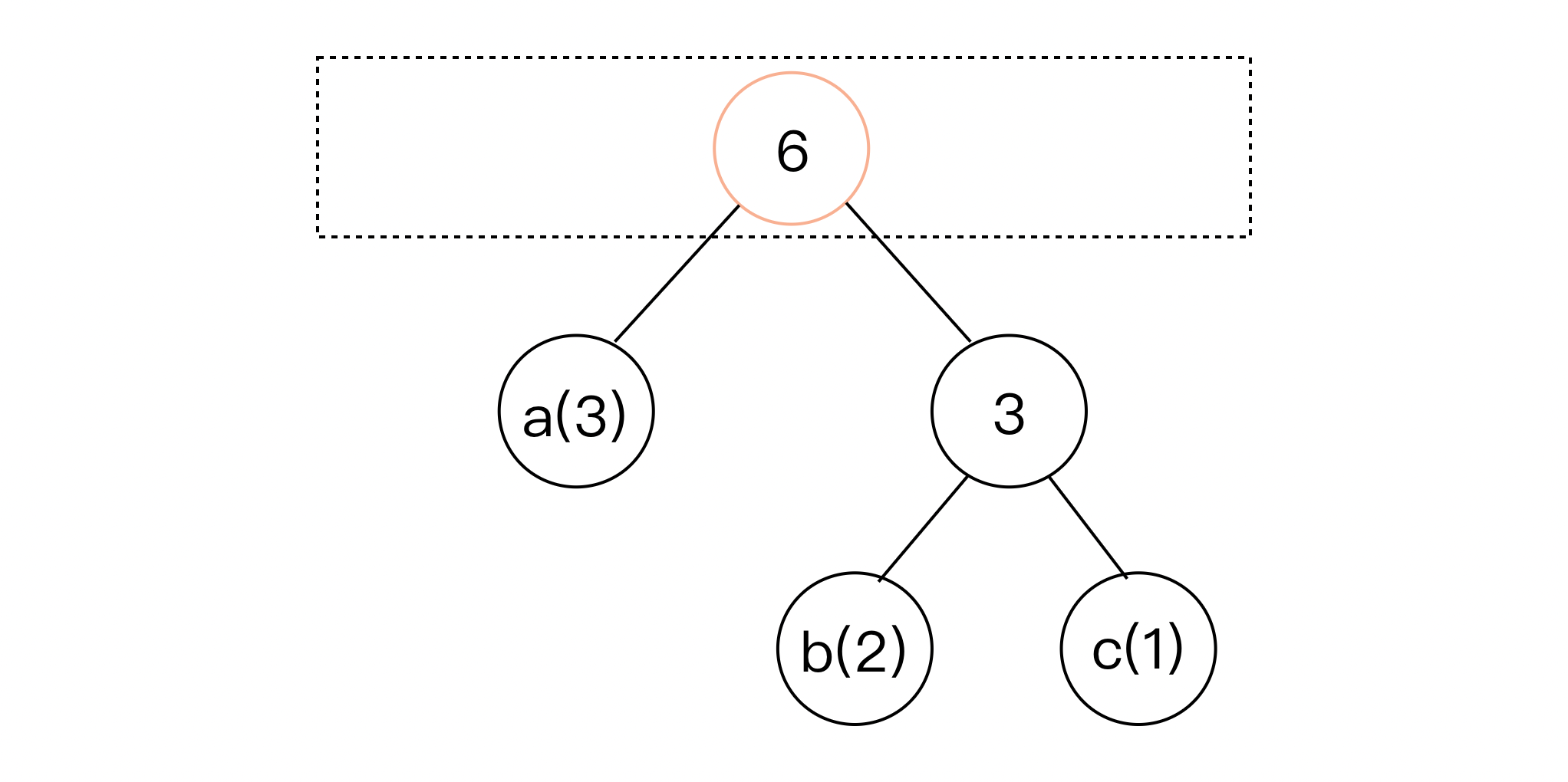
5. 现在，该队列只剩余一个节点，即根节点。至此，霍夫曼树构建完成。

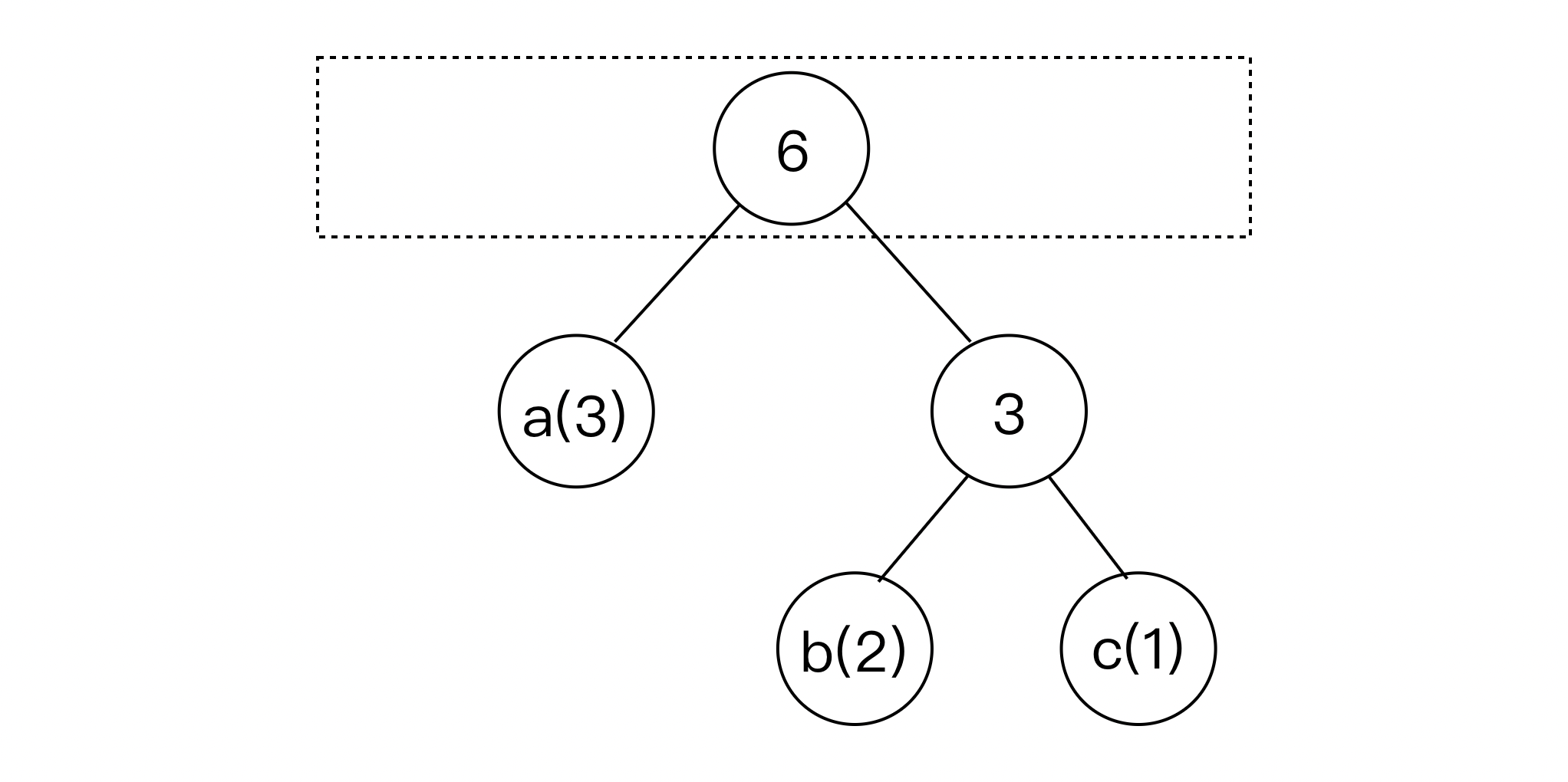
实际上，霍夫曼编码使用了贪心算法。

贪心算法是一种解决问题的策略，它在每一步都做出局部最优选择，以实现全局最优解。换句话说，它在每一步都选择最佳选项，而不考虑该选择的长期影响。虽然贪心算法并不总是保证最优解，但它可以在合理的时间复杂度内解决许多问题。

对于霍夫曼编码，贪心算法被用来构建一个二叉树，使编码长度最小。它通过分析数据中每个字符或符号的出现频率，并为出现频率较高的字符分配较短的代码来实现这一点。算法首先构建输入数据中所有字符的频率表（步骤1）。然后，它为每个字符创建一个叶节点，其频率等于字符在输入数据中的频率（步骤2）。

而步骤3，正是贪心算法大展身手的地方。算法先选取频率最低的两个节点，并将它们合并成一个频率等于它们频率之和的新节点。这个新节点成为二叉树中两个原始节点的父节点。该算法重复这一步，直到树中只剩下一个节点，该节点成为树的根节点。

通过反复做出合并频率最低的两个节点的局部最优选择，贪心算法构建了一个霍夫曼树，稍后，树根据每个符号出现的频率为它们生成最短的可变长度编码。这就是贪心算法的力量所在：通过在每一步做出局部最优选择，它为数据压缩产生了全局最优解决方案。

但我们同时提到，“贪心算法并不总是保证最优解”，因此，稍后我们将给出贪心算法在霍夫曼编码中的最优性证明。

while (nodes.length > 1) {
  nodes.sort((a, b) => a.freq - b.freq);

  let left = nodes.shift();
  let right = nodes.shift();

  let newNode = {
    char: null,
    freq: left.freq + right.freq,
    left: left,
    right: right,
  };

  nodes.push(newNode);
}

4. 生成可变长度编码表

成功构建霍夫曼树后，我们便可以遍历霍夫曼树，为每个字符生成可变长度编码。具体来说，从根节点开始遍历的过程中，我们可以将左子节点标记为 0 ，右子节点标记为 1 ，直至遍历到叶子节点，从而生成每个字符的编码。

例如，对于样例中字符串对应的霍夫曼树中，字符编码表为：

字符	搜索叶子结点路径	可变长度编码
a	左	0
b	右 左	10
c	右 右	11

特别的是，在实践中，也有其他的编码方式，例如将左子节点标记为 1 ，右子节点标记为 0 ，或者使用其他符号代替 0 和 1 。不过，由于左0右1的编码方式在实践中已经被广泛采用和验证，因此我们通常会选择使用这种方式来生成霍夫曼编码。

let codes = {};

function traverse(node, code) {
  if (node.char) {
    codes[node.char] = code;
  } else {
    traverse(node.left, code + "0");
    traverse(node.right, code + "1");
  }
}
let root = nodes[0];
traverse(root, "");

5. 获得压缩编码

根据原文件数据及生成的可变长度编码，获得压缩编码。

let compressed = "";

for (let i = 0; i < str.length; i++) {
  let char = str.charAt(i);
  compressed += codes[char];
}

经过以上5个步骤，我们终于得到了压缩编码，对于我们样例代码中的字符串 aaabbc ，其对应的压缩编码，亦即霍夫曼编码为：

000101011

由此可见，霍夫曼编码的长度远小于原字符串的编码长度。在我们的样例中，6个字符组成的字符串只占用了9个比特，两字节都不到！

解码

前面提到，霍夫曼编码是一种前缀编码，即任何一个字符的编码都不是另一个字符编码的前缀，因此可以通过编码唯一地解码出原始数据。解码霍夫曼编码需要使用「步骤3」中构建好的霍夫曼树。

对于给定的霍夫曼编码，我们可以从根节点开始，依次遍历编码中的每一位，如果该位为0，则向左子树移动，如果该位为1，则向右子树移动，直至到达叶子节点，亦即找到对应的字符。

function decodeHuffmanCode(huffmanCode, huffmanTree) {
  let decodedStr = "";
  let currentNode = huffmanTree;

  for (let i = 0; i < huffmanCode.length; i++) {
    if (huffmanCode[i] === "0") {
      currentNode = currentNode.left;
    } else {
      currentNode = currentNode.right;
    }

    if (currentNode.left === null && currentNode.right === null) {
      decodedStr += currentNode.char;
      currentNode = huffmanTree;
    }
  }

  return decodedStr;
}

例如，对于我们在「编码流程」中生成的 000101011 ，使用以上的解码方法，将得到字符串：

aaabbc

可以看到，该字符串与我们一开始进行霍夫曼编码的原始信息完全相等。

最优性证明

命题：

霍夫曼 编码为最优的前缀编码，亦即没有期望长度比它更小的前缀编码。

证明：

记某一长度为 $n$ 的字符集 $\{s_1, s_2, ..., s_n\}$ 为 $M$ ，字符集中字符的对应频率为 $\{f_1, f_2, ..., f_n\}$。记 $L$ 为 $M$ 的比特长度。我们希望使用可变长度编码对 $M$ 进行编码，从而使得 $L$ 的期望值最小。

设 $C$ 为 霍夫曼 编码算法生成的前缀编码。则其编码长度为：

$$L(C) = f_1 \cdot l_1 + f_2 \cdot l_2 + ... + f_n \cdot l_n$$

其中，$l_i$ 是编码 $C$ 中字符 $s_i$ 的编码长度。

现在，假设 $D$ 为除 $C$ 之外 $M$ 的任意前缀编码。则我们需要证明 $D$ 的编码长度大于或等于 $C$ 的编码长度。

由于 $D$ 是一个前缀编码，则其满足 Kraft-McMillan 不等式，即：

$$\sum_{i=1}^n 2^{-l_i} \leq 1$$

其中，$l_i$ 是编码 $D$ 中字符 $s_i$ 的编码长度。

此时，两边同乘 $f_i$ 并对 $i$ 求和, 即可得到：

$$\sum_{i=1}^n f_i \cdot 2^{-l_i} \leq \sum_{i=1}^n f_i$$

接着，使用 Jensen 不等式，我们可以得到：

$$\sum_{i=1}^n f_i \cdot 2^{-l_i} \geq 2^{-L(D)}$$

其中， $L(D)$ 是 $D$ 的编码长度。

于是，我们得到：

$$2^{-L(D)} \leq \sum_{i=1}^n f_i$$

两边同乘 $L(D)$ ，并基于 $x \log_2 x \leq 1$ ，可得：

$$L(D) \geq \log_2 \left( \sum_{i=1}^n f_i \right)$$

现在，由 $C$ 为霍夫曼编码，我们有：

$$\sum_{i=1}^n f_i \cdot 2^{-l_i} \geq \sum_{i=1}^n f_i \cdot 2^{-c_i}$$

其中，$c_i$ 是编码 $C$ 中字符 $s_i$ 的编码长度。

使用 Kraft-McMillan 不等式，我们可以得到：

$$\sum_{i=1}^n 2^{-c_i} \leq 1$$

两边同乘 $f_i$ 并对 $i$ 求和，可得：

$$\sum_{i=1}^n f_i \cdot 2^{-c_i} \leq \sum_{i=1}^n f_i$$

因此，我们最终得到：

$$L(D) \geq \log_2\left(\sum_{i=1}^{n} f_i\right) \geq L(C)$$

该不等式向我们表明：任何除 $C$ 之外的前缀编码，其期望长度都大于或等于 $C$ ，因此，霍夫曼编码为最优的前缀编码，没有其他前缀编码的期望长度比它更小。

小结

现在你知道，霍夫曼编码是由David A. Huffman于1952年发明的一种无损数据压缩技术。该编码为使用贪心算法及二叉树为数据中的字符或符号生成的可变长度编码。其中，频率最高的字符或符号分配最短码，频率最低的字符或符号分配最长码。而在其最优性的证明中，Kraft-McMillan 不等式起到了关键作用。